개요
이전 포스팅에서는 MDP를 사용하여 순차적 행동 결정 문제를 정의했습니다. 이제 에이전트는 이 MDP를 이용하여 최적 정책을 찾으면 됩니다.
하지만 에이전트가 어떻게 최적 정책을 찾을 수 있을까요?
가치함수
최적 정책을 찾으려면 에이전트가 어떤 상태에서 앞으로 받을 보상들을 고려해 높은 보상을 얻는 행동들을 선택하면 될 것입니다. 이 앞으로 받을 보상에 대한 개념이 바로 가치함수입니다.
즉 에이전트는 가치함수를 통해 행동을 선택할 수 있는 것이죠.

상태 가치함수
단순히 앞으로 받을 보상들의 합을 표현하면 다음과 같습니다.
$$R_{t+1} + R_{t+2} + R_{t+3} + R_{t+4} + R_{t+5} + ... $$
하지만 저희는 이전 포스팅에서 MDP의 구성요소 중 하나인 할인율 $γ$에 대해서 배웠기 때문에 위와 같이 표현하면 안된다는 것을 알 수 있을 것입니다.
할인율을 적용한 보상들의 합은 다음과 같습니다.
$$R_{t+1} + γR_{t+2} + γ^2R_{t+3} + γ^3R_{t+4} + γ^4R_{t+5} + ... $$
위 식의 값을 반환값 $G_t$라고 합니다.
$$G_t = R_{t+1} + γR_{t+2} + γ^2R_{t+3} + γ^3R_{t+4} + γ^4R_{t+5} + ... $$
반환값이라는 것은 에이전트가 실제로 환경을 탐험하며 받은 보상의 합입니다.
즉 다르게 말하면 반환값은 에이전트가 환경과 상호작용을 하다 마지막 상태가 되어야 계산할 수 있다는 것입니다.
이 유한한 에이전트와 환경의 상호작용을 에피소드라고 부릅니다.
에이전트와 환경의 상호작용은 불확실성을 내포하고 있기 때문에 특정 상태의 반환값은 에피소드마다 다를 수 있습니다.
따라서 저희는 특정 상태의 가치(상태 가치함수)를 반환값에 대한 기댓값으로 판단할 수 있습니다.
$$v(s) = E[G_t | S_t = s ]$$
이때 가치함수는 확률변수가 아니라 특정 양을 나타내는 값이므로 소문자로 표현합니다.
위의 식에서 반환값의 수식을 대입하면 다음과 같습니다.
$$v(s) = E[R_{t+1} + γR_{t+2} + γ^2R_{t+3} + ... | S_t = s ] $$
$γR_{t+2}$부터 뒤의 항을 $γ$로 묶고 반환값의 형태로 표현하면 식은 다음과 같이 바뀝니다.
$$v(s) = E[R_{t+1} + γ(R_{t+2} + γR_{t+3} + ...) | S_t = s ]$$
$$v(s) = E[R_{t+1} + γG_{t+1} | S_t = s ]$$
$R_{t+2} + γR_{t+3} + ...$ 부분을 반환값의 형태로 표현하긴 했지만 사실 에이전트가 실제로 탐험하면서 얻은 보상은 아닙니다. 받을 것으로 예상되는 보상이죠.
따라서 이를 가치함수로 표현할 수 있죠.
$$v(s) = E[R_{t+1} + γv(S_{t+1}) | S_t = s ]$$
지금까지는 가치함수를 정의할 때 정책을 고려하지 않았습니다. 하지만 앞으로 받을 보상들의 합이 가치함수의 정의라는 것을 생각해보면 가치함수는 정책과 무관할 수 없습니다.
보상이라는 것은 에이전트가 정책에 따라 행동했을 때 환경으로부터 받는 것이기 때문입니다. 따라서 MDP로 정의되는 문제에서 가치함수는 항상 정책에 의존하게 됩니다.
따라서 수식을 아래와 같이 쓰면 더 정확한 표현이 되겠죠.
$$v_π(s) = E_π[R_{t+1} + γv_π(S_{t+1}) | S_t = s ]$$
위의 최종 식이 강화학습에서 풀어야하는 벨만 기대 방정식입니다. 즉 벨만 기대 방정식은 현재 상태의 가치함수 $v_π(s)$와 다음 상태의 가치함수 $v_π(S_{t+1})$사이의 관계를 말해주는 방정식입니다.
벨만 방정식에 대해서는 이따가 더 자세히 설명하겠습니다.
행동 가치함수(큐함수)
지금까지 설명한 가치함수는 상태가 입력으로 들어왔을 때 그 상태에서 앞으로 받을 보상의 합을 출력하는 상태 가치함수였습니다.
이제 에이전트는 이 상태 가치함수 값이 높은 상태를 목표로 행동을 선택할 것입니다. 행동을 선택해야하기 때문에 어떤 상태에서 어떤 행동이 얼마나 좋은지 알려주는 함수가 있으면 참 좋겠죠.
그래서 등장한 것이 행동 가치함수이고 이를 큐함수라고 부릅니다. 큐함수도 가치함수이기 때문에 "어떤 행동을 했을 때 받을 보상들의 합"입니다.
상태 가치함수는 "어떤 상태에서 앞으로 받을 보상들의 합"이므로 모든 상태에 대해서 각 행동을 할 확률을 나타내는 정책 $π(a | s)$에 큐함수 $q_π(s, a)$를 곱한 값을 더하면 상태 가치함수가 됩니다. 수식으로 나타내면 다음과 같습니다.
$$v_π(s) = \sum_{a∈A} π(a | s) q_π(s, a)$$
아래 예시를 통해서 위 식을 사용해봅시다.
Q. 에이전트가 아래 그림처럼 중앙에 위치해있고 V는 에이전트가 각 화살표 방향으로 행동했을 때의 가치함수입니다. 보상은 오른쪽, 아래로 행동했을 때 각각 0.5, 1씩 주어지고 나머지 행동들은 보상이 0입니다. 할인율은 0.9이고 각 행동을 할 확률은 25%씩이라고 하면 에이전트의 현재 상태가치함수를 구해봅시다.
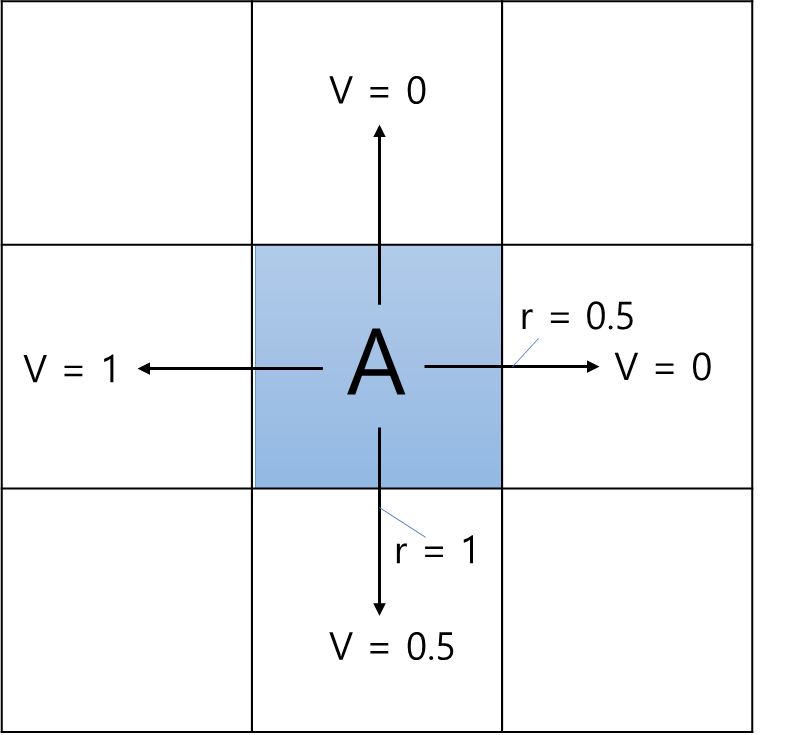
A. 큐함수는 "어떤 행동을 했을 때 받을 보상들의 합"이므로 행동으로 얻는 보상 $r(s,a)$에다가 행동을 한 후 상태에서의 가치함수에 할인율을 곱한 값 $γv_π(s')$을 더하면 큐함수와 같아집니다.
$$q_π(s, a) = r(s,a) + γv_π(s')$$
따라서 현재 에이전트의 상태 가치함수는 다음과 같이 표현할 수 있습니다.
$$v_π(s) = \sum_{a∈A} π(a | s) (r(s,a) + γv_π(s'))$$
이 식을 이용해서 상태 가치함수를 계산하면 다음과 같아집니다.
| 행동 = up | 0.25 x (0 + 0.9 x 0) = 0 |
| 행동 = down | 0.25 x (1 + 0.9 x 0.5) = 0.3625 |
| 행동 = left | 0.25 x (0 + 0.9 x 1) = 0.225 |
| 행동 = right | 0.25 x (0.5 + 0.9 x 0) = 0.125 |
| 총합 | 행동 가치함수 = 0 + 0.3625 + 0.225 + 0.125 = 0.7125 |
단, 위의 경우는 상태 변환 확률을 1일 경우 성립하는 식입니다.(에이전트가 오른쪽으로 가는 행동을 정했을 때 무조건 오른쪽으로 이동하게 되어있음)
상태 변환 확률을 고려한 식은 다음과 같습니다. $$v_π(s) = \sum_{a∈A} π(a | s) (r(s,a) + γ\sum_{s'∈S}P_{ss'} ^a v_π(s'))$$
실제로 이 식은 가치함수를 업데이트하는데 사용되는 식이기도 합니다. 다음 내용에서 더 자세히 알아보죠.
벨만방정식
벨만 기대 방정식
저희는 가치함수를 변형시켜 아래의 식에 해당하는 벨만 기대 방정식을 만들었습니다.
$$v_π(s) = E_π[R_{t+1} + γv_π(S_{t+1}) | S_t = s ]$$
이 방정식은 현재 상태의 가치함수와 다음 상태의 가치함수 사이의 관계를 나타내는 것이죠.
저희는 이제 이 방정식을 푼다면 모든 상태에 대한 가치함수를 구할 수 있습니다. 하지만 생각해보면 이 방정식을 풀기란 쉽지가 않죠.
기댓값을 알아내야하므로 앞으로 받을 모든 보상에 대해 고려해야 합니다.
이는 상태가 많아질수록 비효율적인 방법이죠.
따라서 우리는 한 번에 모든 것을 계산하는 것이 아니라 값을 변수에 저장하고 루프를 도는 계산을 통해 참 값을 알아나가는 방법을 사용합니다.
벨만 기대 방정식에서 좌항과 우항이 같아질 때까지 $v_π(s)$값을 $E_π[R_{t+1} + γv_π(S_{t+1}) | S_t = s ]$로 대체하며 업데이트하는 것입니다.
기댓값을 계산하기 위해서는 위 예시에서 사용했던, 각 행동을 할 확률을 나타내는 정책 $π(a | s)$에 큐함수 $q_π(s, a)( = r(s,a) + γv_π(s'))$를 곱한 값을 더하는 방법을 사용합니다.
$$v_π(s) = \sum_{a∈A} π(a | s) (r(s,a) + γ\sum_{s'∈S}P_{ss'} ^a v_π(s'))$$
그리드월드에서는 상태 변환 확률이 1인 경우만 고려하므로 다음 식을 사용합니다.
$$v_π(s) = \sum_{a∈A} π(a | s) (r(s,a) + γv_π(s'))$$
이제 우리는 이 벨만 기대 방정식을 이용해서 현재의 가치함수를 업데이트하다 보면 참값을 구할 수 있습니다.
이 참값이라는 것은 최대로 받을 보상을 이야기하는 것이 아닌 현재의 정책 $π$에 대한 참 가치함수 값을 뜻합니다.
벨만 최적 방정식
벨만 기대 방정식이 참 가치함수를 구하는 식이라면, 벨만 최적 방정식은 최적 가치함수를 구하는 식입니다.
참 가치함수는 "어떤 정책"을 따라서 움직였을 경우에 받게 되는 보상에 대한 참값이라면, 최적 가치함수는 수많은 정책 중 가장 높은 보상을 얻게 되는 정책(최적 정책)을 따랐을 때의 가치함수입니다.
가치함수는 어떤 정책을 따라갔을 때 받을 보상들의 합이므로 결국 정책이 얼마나 좋은지를 말해줍니다.
따라서 모든 정책에 대해 가장 큰 가치함수를 주는 정책이 최적 정책이며 최적 정책을 따라갔을 때 받을 보상의 합이 최적 가치함수입니다. 이는 최적 큐함수 또한 같습니다. 이를 수식으로 나타내면 다음과 같습니다.
- 최적의 가치함수 $$v_*(s) = max_π[v_π(s)]$$
- 최적의 큐함수 $$q_*(s,a) = max_π[q_π(s,a)]$$
이때 최적 정책은 각 상태 s에서의 최적의 큐함수 중에서 가장 큰 큐함수를 가진 행동을 하는 것입니다. 이 부분이 헷갈릴 수 있는데 최적의 큐함수란 모든 정책에 대해서 어떤 상태에서 어떤 행동을 했을 때 얻는 보상의 합 중 최대값을 뜻합니다.
예를 들어 에이전트가 가능한 행동이 왼쪽(left)과 오른쪽(right)만 있다고 가정할 때 상태 s에서 왼쪽(left)으로 가는 행동의 큐함수 중 최댓값이 3이고 오른쪽(right)으로 가는 행동의 큐함수의 최댓값이 5라고 합시다.
이때 각 행동의 큐함수 최댓값이 최적의 큐함수가 되는 것이죠. ($q_*(s,left) = 3$와 $q_*(s,right) = 5$)
그리고 이 두 최적의 큐함수 중에서 가장 큰 값인 오른쪽으로 가는 행동을 해야, 보상의 합을 최대로 만드는 최적 정책이 될 것입니다.
이를 수식으로 표현하면 다음과 같습니다.
$$π_*(s,a) = \begin{cases} 1 &\text{ if } a = argmax_{a∈A}q_*(s,a)\\ 0 &otherwise\end{cases} $$
$argmax$는 $q_*$를 최대로 해주는 행동 a를 반환하는 함수입니다.
즉 큐함수가 최적의 큐함수가 아니라면 에이전트가 큐함수 중 최대를 선택해도 가치함수는 최적의 가치함수가 되지 않습니다. 따라서 최적의 큐함수 중 max를 취하는 것이 최적의 가치함수가 됩니다.
$$v_*(s) = \underset{a}{max}[q_*(s,a) | S_t = s, A_t = a]$$
위의 큐함수를 가치함수로 고쳐서 표현하면 다음과 같습니다.
$$v_*(s) = \underset{a}{max}E[R_{t+1} + γv_*(S_{t+1}) | S_t = s, A_t = a]$$
우리는 위의 식을 벨만 최적 방정식이라 부르며 이 식은 최적의 가치함수에 대한 것입니다. 이 때 식에 기댓값 E가 포함된 이유는 상태 변환 확률을 고려했기 때문입니다.
그렇지만 이를 고려하면 어떤 행동으로 변할 수 있는 모든 상태에 대한 가치함수까지 고려해야 하기 때문에 계산이 엄청나게 복잡해지게 됩니다. 따라서 앞으로 나올 모든 예제에서는 상태 변환 확률을 1이라 가정하고 기댓값 E를 생략한 벨만 최적 방정식을 사용합니다.
다음 포스팅에서는 다이내믹 프로그래밍을 이용하여 지금까지 배운 벨만 기대 방정식, 벨만 최적 방정식을 계산으로 푸는 방법과 이 두 방정식으로 어떻게 최적 정책을 찾아내는지 코드 예시와 함께 설명할 예정입니다.
오늘도 긴 글 읽어주셔서 감사합니다~!

http://www.yes24.com/Product/Goods/44136413
파이썬과 케라스로 배우는 강화학습 - YES24
“강화학습을 쉽게 이해하고 코드로 구현하기”강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다!‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지기
www.yes24.com
※ 이 글은 위의 책 내용을 바탕으로 작성한 글입니다.
'강화학습 > 파이썬과 케라스로 배우는 강화학습(스터디)' 카테고리의 다른 글
| [강화학습] 06 - 몬테카를로와 시간차 예측 (2) | 2022.12.24 |
|---|---|
| [강화학습] 05 - 그리드월드와 다이내믹 프로그래밍 (2) (5) | 2022.12.22 |
| [강화학습] 04 - 그리드월드와 다이내믹 프로그래밍 (1) (0) | 2022.12.19 |
| [강화학습] 02 - MDP (0) | 2022.12.13 |
| [강화학습] 01 - 강화학습 개요 (0) | 2022.12.12 |