개요
지금까지 저희는 순차적 행동 결정 문제에서 MDP를 정의하고 벨만 방정식을 세우는 과정을 다뤘습니다.
저희가 이제 해야할 것은 이 벨만 방정식을 이용해서 순차적 행동 결정 문제의 목표인 최적 가치함수와 최적 정책을 찾는 것입니다.

그 방법 중 하나가 바로 강화학습이죠!! 하지만 강화학습 이전에 벨만 방정식을 푸는 알고리즘이 존재했는데 그것이 바로 다이내믹 프로그래밍입니다.
다이내믹 프로그래밍은 이후 강화학습의 근간이 되었기 때문에 저희는 강화학습을 보다 잘 이해하기 위해서 이번 포스팅에서는 다이내믹 프로그래밍과, 벨만 방정식을 푸는 방법을 그리드 월드 예제를 통해서 살펴보겠습니다.
다이내믹 프로그래밍
코딩을 해보거나 알고리즘에 대해서 공부해봤다 하시는 분들은 이 다이내믹 프로그래밍을 한번 쯤은 들어봤을 겁니다.
다이내믹 프로그래밍의 기본적인 아이디어는 큰 문제 안에 작은 문제들이 중첩된 경우에 전체 큰 문제를 작은 문제로 쪼개서 풀겠다는 것입니다.
이때 각각의 작은 문제들이 별개가 아니기 때문에 작은 문제들의 해답을 서로서로 이용할 수 있습니다. 결과적으로 계산량을 줄일 수 있는 것이죠.
예를 들어 어떤 MDP로 정의된 문제의 전체 상태집합이 다음과 같다고 합시다. $$S = \{s_1, s_2, s_3\}$$ 원래대로라면 우리는 아래 그림과 같이 $s_1$의 가치함수를 계속 업데이트 시키며 참 가치함수를 구하면 다음 $s_2$의 계속 가치함수를 업데이트시키며 참 가치함수를 구하는 식으로 순서대로 현재 정책에 대한 참 가치함수를 구해야합니다.
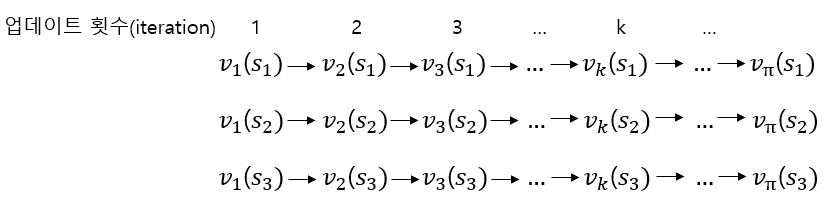
하지만 다이내믹 프로그래밍을 쓰면 아래 그림과 같이 한번에 모든 상태에 대해서 가치함수 값(작은 문제)을 한 번 업데이트를 하고, 이 업데이트된 가치함수를 이용해서 다시 모든 상태에 대한 가치함수를 업데이트하는 과정을 반복하면서 참 가치함수(큰 문제)를 구하게 됩니다. 이때 이전 가치함수 값을 이용하므로 계산량이 확 줄어드는 것이죠.
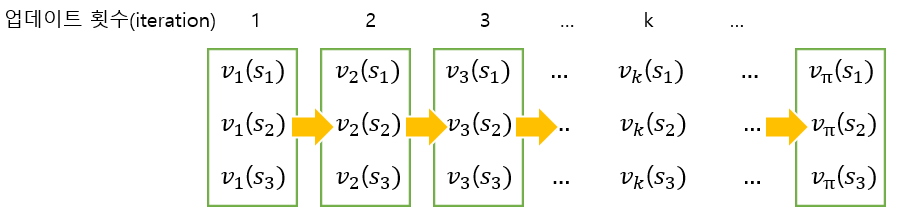
이러한 다이내믹 프로그래밍에는 정책 이터레이션과 가치 이터레이션이 있습니다.
다이내믹 프로그래밍으로 벨만 기대 방정식을 푸는 것이 정책 이터레이션이며 벨만 최적 방정식을 푸는 것이 가치 이터레이션입니다.
저희는 이 2가지 다이내믹 프로그래밍 방법으로 어떻게 벨만 방정식을 푸는지 그리드월드 예제 코드를 이용해서 살펴보려고 합니다.
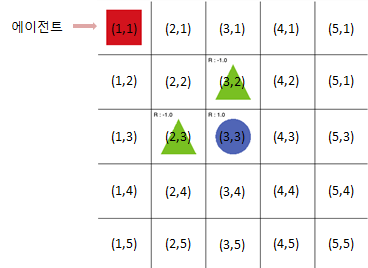
빨간색 네모: 에이전트
파란색 동그라미: 목표(가야할 곳)
연두색 세모: 장애물
에이전트가 연두색으로 가면 (-1)의 보상을 받고,
파란색에 도착하면 (+1)의 보상을 받는다.
에이전트가 파란색에 도착하는 최적 정책을 찾는 것이 목표
정책 이터레이션
MDP로 정의되는 문제에서 결국 구하고자 하는 것은 최적 정책입니다. 하지만 초기에는 이 정책을 알 수가 없죠.
따라서 보통 처음에는 무작위로 행동을 정하는 정책으로부터 시작하여 현재의 정책을 "평가"하고 더 나은 정책으로 "발전"시켜나가는 방법을 사용합니다.
정책 이터레이션에서는 평가를 정책 평가라고 하며, 발전을 정책 발전이라고 합니다.
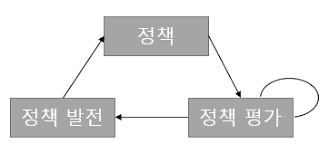
현재 정책을 평가하고 더 나은 정책으로 발전시키는 과정을 무한히 반복하면 정책은 최적 정책으로 수렴하게 됩니다.
정책 평가
그렇다면 정책을 어떻게 평가할 수 있을까요? 우리는 정책을 평가하기 아주 적합한 함수를 미리 배웠습니다.
바로 가치함수이죠. 가치함수는 현재 정책을 따라갔을 때 받을 보상에 대한 기댓값이기 때문에 좋은 판단 기준이 됩니다.
정책 이터레이션은 이 가치함수를 다이내믹 프로그래밍을 이용하여 구하기 위해서 벨만 기대 방정식을 사용합니다. $$v_π(s) = E_π[R_{t+1} + γv_π(S_{t+1}) | S_t = s ]$$
핵심은 주변 상태의 가치함수($v_π(S_{t+1})$)와 한 타임스템의 보상($R_{t+1}$)만 고려해서 현재 상태의 다음 가치함수($v_π(s)$)를 계산하겠다는 것입니다.
이때 주변 상태의 가치함수들은 여러번 업데이트된 가치함수가 아니므로 참 가치함수가 아닙니다.
따라서 이를 이용해서 구한 현재 상태의 다음 가치함수도 참 값이 아니죠. 하지만 이 계산을 여러 번 반복하면 참 값으로 수렴하는 것입니다.
컴퓨터는 기댓값을 계산하지 못하기 때문에 벨만 기대 방정식을 다음과 같이 정책과 큐함수의 곱으로 바꿔봅시다. (그리드 월드에서는 상태 변환 확률이 1) $$v_π(s) = \sum_{a∈A} π(a | s) (r(s,a) + γv_π(s'))$$ 이 과정 또한 이전 벨만 방정식 파트에서 설명했으니 이해가 잘 될 것입니다.
우리는 다이내믹 프로그래밍을 사용하므로 $π$라는 정책에 대해 정책 평가를 반복적으로 수행합니다. 따라서 계산의 단계를 표현할 새로운 변수 k = 1, 2, 3, 4, ...를 이용하여 벨만 기대 방정식을 바꿔주면 다음과 같습니다. $$v_{k+1}(s) = \sum_{a∈A} π(a | s) (r(s,a) + γv_k(s'))$$ 이를 그림으로 표현하면 다음과 같습니다.

그림처럼 현재 상태(하늘색)의 가치함수를 한 타임스텝 보상과 다음 상태(보라색)의 가치함수만을 고려해서 계산한 후 가치함수를 업데이트하는 것이죠. 그리고 이 과정을 모든 상태에 대해 반복하면서 현 정책에 대한 참 가치함수를 구하는 것입니다.
정책 발전
정책 평가만을 반복한다면 현재 정책에 대한 참 가치함수에만 근접할 뿐 최적 정책을 찾을 수는 없습니다. 우리는 정책 평가를 마쳤다면 정책을 발전시켜야 합니다.
정책 발전의 방법이 정해져있지는 않지만 이 책에서는 가장 널리 알려진 탐욕 정책 발전을 사용합니다. 이는 우리가 앞에서 배운 큐함수 즉 행동 가치함수를 사용합니다. 큐함수란 어떤 상태에서 어떤 행동을 했을 때 얻게 될 보상들의 합으로 다음과 같이 표현했습니다. $$q_π(s, a) = r(s,a) + γv_π(s')$$
탐욕 정책 발전은 어떤 상태 s에 대한 큐함수 중 가장 큰 큐함수를 가지는 행동만을 선택하는 방법입니다. 눈 앞에 보이는 것 중에서 당장에 가장 큰 이익을 추구하는 것이죠.
따라서 정책 발전을 통해 업데이트된 정책은 다음과 같습니다. $$π'(s) = argmax_{a∈A}q_π(s, a)$$ 이 탐욕 정책 발전을 사용하면 단기적으로 무조건 이익을 보며 장기적으로는 최적 정책에 수렴할 수 있습니다.
정책 이터레이션 코드 설명
다이내믹 프로그래밍에서 에이전트는 환경의 모든 정보를 알고 있습니다. 에이전트는 이 환경의 정보를 이용하여 최적 정책을 찾는 계산을 하는 것입니다.
계산에 필요한 정보와 함수는 Env라는 클래스로 정의돼 있습니다.
| 코드 | 설명 | 반환값 | |
| 1 | env.width, env.height | 그리드월드의 너비와 높이 | 그리드월드의 가로, 세로를 정수로 반환 |
| 2 | env.state_after_action(state, action) | 특정 상태에서 특정 행동을 했을 때 에이전트가 가는 다음 상태 | 행동 후의 상태를 좌표로 표현한 리스트를 반환 ex) [1,2] |
| 3 | env.get_all_states() | 존재하는 모든 상태 | 모든 상태를 반환 ex) [[0,0],[0,1],...,[4,4]] |
| 4 | env.get_reward(state, action) | 특정 상태에서 특정 행동을 했을 때 얻는 보상 | 정수의 형태로 보상을 반환 |
| 5 | env.possible_actions | 에이전트가 가능한 행동(상, 하, 좌, 우) | [0,1,2,3]을 반환, 순서대로 상, 하, 좌, 우를 의미 |
위의 표는 Env 클래스 안에 정의되어 있는 환경의 정보를 나타낸 것입니다.
이제 환경의 정보를 이용하여 표현된, 정책 이터레이션의 정책 평가와 정책 발전의 소스코드를 자세히 살펴봅시다.
import numpy as np
from environment import GraphicDisplay, Env다차원 배열을 처리하기 위해 numpy를 np로 import를 하고 환경의 정보를 사용하기 위해 Env, GUI로 그리드월드 환경을 보여주기 위해 GraphicDisplay 클래스를 import합니다.
<변수 선언>
def __init__(self, env):
# 환경에 대한 객체 선언
self.env = env
# 가치함수를 2차원 리스트로 초기화
self.value_table = [[0.0] * env.width for _ in range(env.height)]
# 상 하 좌 우 동일한 확률로 정책 초기화
self.policy_table = [[[0.25, 0.25, 0.25, 0.25]] * env.width
for _ in range(env.height)]
# 마침 상태의 설정
self.policy_table[2][2] = []
# 할인율
self.discount_factor = 0.9
모든 상태에 대한 가치함수를 value_table이라는 2차원 리스트 변수로 가치함수를 선언합니다.
policy_table은 모든 상태에 대해 상, 하, 좌, 우에 해당하는 각 행동을 할 확률을 담고 있는 5 x 5 x 4 크기의 3차원 리스트입니다. 정책의 초기값은 4가지 행동 중 무작위로 행동을 결정하도록 25%씩 [0.25, 0.25, 0.25, 0.25]로 설정합니다. policy_table[2][2]는 목표점이 있는 좌표이므로 에이전트가 이곳에 도착하면 정책은 무의미하기 때문에 빈리스트를 할당해줍니다.
할인율 discount_factor는 0.9로 정의합니다.
<policy_evaluation(정책 평가)>
# 벨만 기대 방정식을 통해 다음 가치함수를 계산하는 정책 평가
def policy_evaluation(self):
# 다음 가치함수 초기화
next_value_table = [[0.00] * self.env.width
for _ in range(self.env.height)]
# 모든 상태에 대해서 벨만 기대방정식을 계산
for state in self.env.get_all_states():
value = 0.0
# 마침 상태의 가치 함수 = 0
if state == [2, 2]:
next_value_table[state[0]][state[1]] = value
continue
# 벨만 기대 방정식
# 가능한 모든 행동에 대해서, 정책(self.get_policy(state)[action])과
# 큐함수(reward + self.discount_factor * next_value)를 곱한 후에 더해줌
for action in self.env.possible_actions:
next_state = self.env.state_after_action(state, action)
reward = self.env.get_reward(state, action)
next_value = self.get_value(next_state)
value += (self.get_policy(state)[action] *
(reward + self.discount_factor * next_value))
# 가치함수를 테이블에 저장
next_value_table[state[0]][state[1]] = value
# 새로운 가치함수 값으로 업데이트
self.value_table = next_value_table$$v_{k+1}(s) = \sum_{a∈A} π(a | s) (r(s,a) + γv_k(s'))$$
정책 평가는 위의 벨만 기대 방정식을 이용해서 한번에 모든 상태의 가치함수 값을 업데이트시켜 나간다고 했습니다.
next_value_table을 선언한 다음 모든 상태(목표인 (2,2)는 제외)에 대한 벨만 기대 방정식의 계산 결과, 즉 가치함수를 next_value_table에 저장합니다.
이후 현재의 value_table에 next_value_table을 덮어쓰는 식으로 정책 평가를 진행합니다.
<policy_improvement(정책 발전)>
# 현재 가치 함수에 대해서 탐욕 정책 발전
def policy_improvement(self):
next_policy = self.policy_table
for state in self.env.get_all_states():
if state == [2, 2]:
continue
value_list = []
# 반환할 정책 초기화
result = [0.0, 0.0, 0.0, 0.0]
# 모든 행동에 대해서 [보상 + (할인율 * 다음 상태 가치함수)] 계산
for index, action in enumerate(self.env.possible_actions):
next_state = self.env.state_after_action(state, action)
reward = self.env.get_reward(state, action)
next_value = self.get_value(next_state)
value = reward + self.discount_factor * next_value
value_list.append(value)
# 받을 보상이 최대인 행동들에 대해 탐욕 정책 발전
# 가장 큰 큐함수의 index를 max_idx_list에 저장
max_idx_list = np.argwhere(value_list == np.amax(value_list))
# 2차원 배열을 1차원 리스트로 바꿔줌
max_idx_list = max_idx_list.flatten().tolist()
# 각 행동을 선택할 행동을 구하기 위해서 1을 max_idx_list의 길이로 나눠줌.
prob = 1 / len(max_idx_list)
for idx in max_idx_list:
result[idx] = prob
# 해당하는 상태의 정책 업데이트
next_policy[state[0]][state[1]] = result
# 전체 정책 업데이트
self.policy_table = next_policy정책 발전에서는 탐욕 정책 발전을 사용해서 모든 상태에 대해서 가장 큰 큐함수를 가진 행동만을 선택하도록 정책을 바꿔준다고 했습니다. $$q_π(s, a) = r(s,a) + rv_π(s')$$
위와 같은 큐함수 식을 이용해서 각 상태에 대해서 가능한 행동들에 대한 큐함수 값을 계산해서 이를 value_list에 저장합니다.
value_list에 들어있는 각 행동들의 큐함수 중 가장 큰 값을 np.amax함수로 알아냅니다. 그리고 np.argwhere 함수를 이용해서 가장 큰 값의 index를 max_idx_list에 저장합니다. 이 때 최대 값이 여러 개라면 여러 개의 index를 반환합니다.
argwhere 함수를 사용하면 반환값이 2차원 배열이 되기 때문에 이를 1차원 리스트로 바꿔주기 위해서 max_idx_list.flatten().tolist()를 사용합니다.
max_idx_list에 담긴 값이 여러 개라면 에이전트는 그 index의 행동들을 동일한 확률에 기반해서 선택합니다. 이를 위해 1을 max_idx_list의 길이로 나눠서 행동의 확률을 계산합니다. 이후 이 계산한 확률값을 next_policy의 해당 상태에 저장합니다.
예를 들어 가장 큰 큐함수를 가진 index가 아래로 가는 행동과 왼쪽으로 가는 행동에 해당하는 1,2로 나왔다면 max_idx_list의 모양은 [1, 2]일 것이고 각 행동을 선택할 확률은 0.5씩이 됩니다. 따라서 result는 [0, 0.5, 0.5, 0]와 같은 모양이 되고 이것이 새로운 정책이 되는 것입니다.
<get_action>
def get_action(self, state):
policy = self.get_policy(state)
policy = np.array(policy)
return np.random.choice(4, 1, p=policy)[0]실제로 에이전트가 현재까지 발전된 정책을 불러오고, 그 정책에 따라서 특정 상태에서 어떤 행동을 할지 결정하는 함수입니다.
np.random.choice(4, 1, p=policy)[0]을 return하는데 이는 현재 정책(p = policy)의 확률에 기반해서 4개의 행동(상, 하, 좌, 우) 중에서 하나의 행동을 고르라는 의미입니다.
정책 이터레이션 코드를 실행하고 정책 평가와 정책 발전을 반복적으로 시행시키면 아래와 같은 최적 정책을 찾을 수 있습니다.
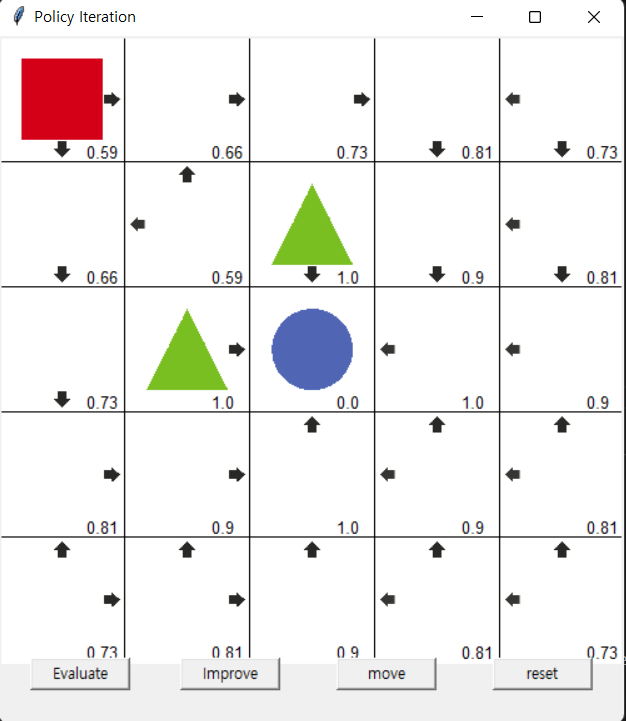
정책 이터레이션의 전체 코드는 아래 링크에서 찾아볼 수 있습니다.
https://github.com/rlcode/reinforcement-learning-kr-v2
GitHub - rlcode/reinforcement-learning-kr-v2: [파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판
[파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판 예제. Contribute to rlcode/reinforcement-learning-kr-v2 development by creating an account on GitHub.
github.com
이렇게 정책 이터레이션의 예제 코드까지 살펴봤는데요. 다음 포스팅에서는 벨만 최적 방정식을 이용해서 MDP로 정의된 문제를 푸는 가치 이터레이션에 대한 설명과 예제 그리고 다이내믹 프로그래밍의 한계에 대해서 설명하겠습니다~!
오늘은 글이 진짜 길어졌는데 지금까지 읽어주셔서 감사드리고욧!! 다음 포스팅에서 뵙겠습니다!!

http://www.yes24.com/Product/Goods/44136413
파이썬과 케라스로 배우는 강화학습 - YES24
“강화학습을 쉽게 이해하고 코드로 구현하기”강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다!‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지기
www.yes24.com
※ 이 글은 위의 책 내용을 바탕으로 작성한 글입니다.
'강화학습 > 파이썬과 케라스로 배우는 강화학습(스터디)' 카테고리의 다른 글
| [강화학습] 06 - 몬테카를로와 시간차 예측 (2) | 2022.12.24 |
|---|---|
| [강화학습] 05 - 그리드월드와 다이내믹 프로그래밍 (2) (5) | 2022.12.22 |
| [강화학습] 03 - 가치함수와 벨만방정식 (2) | 2022.12.16 |
| [강화학습] 02 - MDP (0) | 2022.12.13 |
| [강화학습] 01 - 강화학습 개요 (0) | 2022.12.12 |