개요
지금까지 카트폴 예제에서 에이전트는 왼쪽 혹은 오른쪽 2가지 행동 중 하나만을 선택할 수 있었습니다. 하지만 실제 환경에서 사람은 몇 가지 행동 중에 골라서 행동하는 것이 아니라 어떠한 위치나 방향으로 행동할 수 있습니다.
즉 실제 환경에서 할 수 있는 행동은 이산적으로 분포하는 것이 아니라 연속적으로 분포해 있는 것이죠.
에이전트가 연속적인 행동을 선택하게 하려면 먼저 이산적인 행동을 많이 만드는 방법을 생각해볼 수 있습니다.
선택할 수 있는 이산적인 행동들이 충분히 많다면 에이전트는 마치 연속적인 행동을 할 수 있는 것처럼 만들 수 있습니다.
하지만 이 방법은 에이전트가 고려해야 할 행동들이 너무 많아지기 때문에 학습이 매우 어려워집니다.
따라서 저희는 정책을 연속적인 분포로 만드는 방법을 사용합니다. 이전까지는 정책이 왼쪽으로 가는 행동과 오른쪽으로 가는 행동에 대해 확률이 하나씩 있는 이산적인 형태<ex) [0.2,0.8]>였습니다.
하지만 평균(μ)과 표준편차(σ)로 표현 가능한 정규분포를 사용하면 정책을 연속적인 확률 분포로 만들 수 있습니다. 아래 그림은 평균과 표준편차로 표현된 정규분포들입니다.

그림을 보면 알 수 있듯이 평균은 분포의 중심을 나타내고 표준편차는 분포의 모양을 결정합니다. 표준편차가 클수록 그래프가 평균 중심으로 퍼져있으며 표준편차가 작을수록 평균 중심에 모여있는 것을 확인할 수 있습니다.
즉 평균은 어느 방향으로 얼마나 미는 것이 좋은지 결정하고 표준편차는 얼마나 탐험을 할 것인지를 결정합니다.
결국 저희는 정규분포 형태의 연속적인 정책을 사용하기 때문에 DQN이 아닌 액터-크리틱 알고리즘을 사용해야 합니다. 액터-크리틱이 연속적 행동을 하게 만든 것을 연속적 액터-크리틱이라고 합니다.
연속적 액터-크리틱 코드 설명
액터-크리틱에서 정책의 형태만 연속적인 분포로 바꿨으므로 정책신경망의 출력을 이용한 부분을 제외하고는 대부분 액터-크리틱 코드와 동일합니다.
<정책신경망 정의>
# 정책 신경망과 가치 신경망 생성
class ContinuousA2C(tf.keras.Model):
def __init__(self, action_size):
super(ContinuousA2C, self).__init__()
self.actor_fc1 = Dense(24, activation='tanh')
self.actor_mu = Dense(action_size,
kernel_initializer=RandomUniform(-1e-3, 1e-3))
self.actor_sigma = Dense(action_size, activation='sigmoid',
kernel_initializer=RandomUniform(-1e-3, 1e-3))
self.critic_fc1 = Dense(24, activation='tanh')
self.critic_fc2 = Dense(24, activation='tanh')
self.critic_out = Dense(1,
kernel_initializer=RandomUniform(-1e-3, 1e-3))
def call(self, x):
actor_x = self.actor_fc1(x)
mu = self.actor_mu(actor_x)
sigma = self.actor_sigma(actor_x)
sigma = sigma + 1e-5
critic_x = self.critic_fc1(x)
critic_x = self.critic_fc2(critic_x)
value = self.critic_out(critic_x)
return mu, sigma, value연속적인 정책을 만들기 위해서 평균과 표준편차로 표현되는 정규분포를 사용했기 때문에 평균과 표준편차를 출력할 self.actor_mu와 self.actor_sigma를 정의해줍니다.
평균의 경우 활성함수로 선형함수를 사용하여 출력하고 이후 [-1,1]의 범위를 넘어가는 출력값은 -1 또는 1로 바꿔서 행동합니다.
표준편차는 1이 넘을 경우 오히려 학습에 도움이 안되기 때문에 0과 1사이의 출력값을 가지도록 sigmoid를 활성함수로 사용합니다.

이때 self.actor_mu와 self.actor_sigma의 출력 개수를 뜻하는 action_size가 이전 액터 크리틱처럼 2라고 생각하실 수 있습니다.
하지만 아래 코드와 같이 연속적 액터-크리틱에서는 환경(env)이 액터-크리틱과 똑같지 않고 다른 환경이기 때문에 action_size가 2가 아니라 1입니다.
env = gym.make('CartPoleContinuous-v0')
action_size = env.action_space.shape[0]
즉 평균과 표준편차가 하나씩 출력되는 것이죠. 최종적으로 모델은 연속적 정책을 표현하기 위한 평균(mu)과 표준편차(sigma), 현재 상태에 대한 가치함수 예측값(value)을 return 해줍니다.
<행동 선택>
from tensorflow_probability import distributions as tfd
# 정책신경망의 출력을 받아 확률적으로 행동을 선택
def get_action(self, state):
mu, sigma, _ = self.model(state)
dist = tfd.Normal(loc=mu[0], scale=sigma[0])
action = dist.sample([1])[0]
action = np.clip(action, -self.max_action, self.max_action) # max_action = 1
return action이제 정책신경망의 출력으로 나온 평균과 표준편차 값을 이용해서 정규분포 형태의 연속적 정책을 만들어야합니다. 만들어진 정책을 이용해 에이전트는 행동을 결정하겠죠.
텐서플로에서는 tensorflow_probability라는 확률 분포와 관련된 코드를 제공하는데, 이 중 distributions라는 클래스 안에 Normal이라는 함수는 loc에 평균값을 인자로 받고, scale에 표준편차 값을 인자로 받아 정규분포를 만들 수 있습니다.
정책신경망의 출력과 Normal함수를 이용해 dist라는 정규분포 형태의 정책을 만들었다면 sample 함수를 이용해 행동을 분포에 따라서 무작위로 추출할 수 있습니다.
1개의 행동만을 구하기 위해 dist.sample([1])을 사용하고, 최종 action이 [-1,1]의 범위를 넘어가면 clip 함수를 이용해 -1 또는 1로 치환해줍니다.
<연속적 액터-크리틱의 학습>
# 각 타임스텝마다 정책신경망과 가치신경망을 업데이트
def train_model(self, state, action, reward, next_state, done):
model_params = self.model.trainable_variables
with tf.GradientTape() as tape:
mu, sigma, value = self.model(state)
_, _, next_value = self.model(next_state)
target = reward + (1 - done) * self.discount_factor * next_value[0]
# 정책 신경망 오류 함수 구하기
advantage = tf.stop_gradient(target - value[0])
dist = tfd.Normal(loc=mu, scale=sigma)
action_prob = dist.prob([action])[0]
cross_entropy = - tf.math.log(action_prob + 1e-5)
actor_loss = tf.reduce_mean(cross_entropy * advantage)
# 가치 신경망 오류 함수 구하기
critic_loss = 0.5 * tf.square(tf.stop_gradient(target) - value[0])
critic_loss = tf.reduce_mean(critic_loss)
# 하나의 오류 함수로 만들기
loss = 0.1 * actor_loss + critic_loss
# 오류함수를 줄이는 방향으로 모델 업데이트
grads = tape.gradient(loss, model_params)
self.optimizer.apply_gradients(zip(grads, model_params))
return loss, sigma연속적 액터-크리틱의 학습 방법은 액터-크리틱과 동일하게 아래 식들을 이용해서 정책신경망과 가치신경망을 업데이트합니다.
$$θ_{t+1} ∽ θ_t - α[∇_θ(-logπ_θ(a | s)δ_v)]$$
MSE = $($정답 - 예측$)^2$ = $(R_{t+1} + γV_v(S_{t+1}) - V_v(S_t))^2$
이때 정책신경망에서 구해야하는 $p_{action}$은 tensorflow_probability에서 제공하는 prob 함수를 사용하면 됩니다.
dist를 확률분포로 만들고 dist.prob([action])을 쓰면 현재 한 행동 action에 해당하는 확률값을 구할 수 있습니다. 이후 과정은 액터-크리틱과 동일합니다.
<주의할 점>
tensorflow_probability를 처음 사용하기 때문에 이를 설치해주어야합니다.
Anaconda Prompt 창에 <pip install tensorflow_probability>를 입력하면 되는데, 현재 자신의 tensorflow의 버전이 2.1.0이라면 코드가 돌아가지 않는 문제가 발생할 것입니다.
이는 tensorflow 버전에 따라 호환되는 tensorflow_probability 버전의 제한이 있기 때문인데요. 자세한 것은 아래 링크에서 확인할 수 있습니다.
https://github.com/tensorflow/probability/releases
Releases · tensorflow/probability
Probabilistic reasoning and statistical analysis in TensorFlow - tensorflow/probability
github.com
tensorflow_probability가 0.9.0 버전이 tensorflow 2.1.0 버전에서 문제없이 돌아가기 때문에 Anaconda Prompt 창에 다음을 입력해 tensorflow_probability를 설치해야 오류가 발생하지 않습니다.
pip install tensorflow-probability==0.9.0
연속적 액터-크리틱의 전체 코드는 아래 링크에서 확인하실 수 있습니다.
https://github.com/rlcode/reinforcement-learning-kr-v2
GitHub - rlcode/reinforcement-learning-kr-v2: [파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판
[파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판 예제. Contribute to rlcode/reinforcement-learning-kr-v2 development by creating an account on GitHub.
github.com
연속적 액터-크리틱 실행 및 결과

연속적 액터-크리틱을 실행하면 터미널 창은 다음과 같이 에피소드마다 평균 점수(score avg), 오류함수(loss), 표준편차(sigma) 값이 출력되는 것을 확인할 수 있습니다.
sigma 값은 에이전트가 얼마나 탐험하고 있는지를 나타내줍니다.

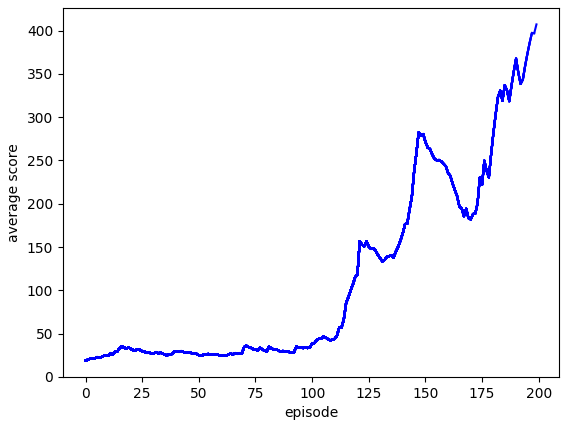
위 그림은 액터-크리틱과 연속적 액터-크리틱을 평균 점수가 400점이 넘을 때까지 실행시킨 것을 에피소드에 따른 평균 점수 그래프로 나타낸 것입니다.
연속적 액터-크리틱은 연속적인 정책을 사용하기 때문에 일정한 거리를 움직이는 액터-크리틱보다 학습 과정이 좀 더 불안한 것을 확인할 수 있습니다. 하지만 둘의 학습하는 데 걸리는 시간은 비슷한 것을 볼 수 있죠.
액터-크리틱과 연속적 액터-크리틱은 크리틱을 업데이트하는 데 살사 방식을 사용하기 때문에 다른 정책에 의해 생성된 샘플로 학습할 수 없습니다. (DQN과 다른 점)
그렇기에 에이전트가 안 좋은 상황에 빠져버리면 잘못된 학습을 하거나 성능이 떨어진다는 단점이 있습니다. 이 단점을 극복한 것이 A3C(Asynchronous Advantage Actor-Critic)입니다.
다음 포스팅부터는 이 A3C에 대해서 설명하도록 하겠습니다. 오늘도 읽어주셔서 감사합니다~!

http://www.yes24.com/Product/Goods/44136413
파이썬과 케라스로 배우는 강화학습 - YES24
“강화학습을 쉽게 이해하고 코드로 구현하기”강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다!‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지기
www.yes24.com
※ 이 글은 위의 책 내용을 바탕으로 작성한 글입니다.
'강화학습 > 파이썬과 케라스로 배우는 강화학습(스터디)' 카테고리의 다른 글
| [강화학습] 16 - Breakout DQN (0) | 2023.01.29 |
|---|---|
| [강화학습] 15 - 브레이크아웃과 CNN (1) | 2023.01.27 |
| [강화학습] 13 - 액터-크리틱 (0) | 2023.01.18 |
| [강화학습] 12 - DQN 알고리즘(Cartpole) (0) | 2023.01.11 |
| [강화학습] 11 - REINFORCE 알고리즘 (1) | 2023.01.08 |