개요
지금까지 저희가 배운 강화학습은 가치함수를 기반으로 행동을 선택하고 학습하는 가치 기반 강화학습이었습니다.
하지만 가치함수를 토대로 행동을 선택하지 않고 상태에 따라 정책으로 바로 행동을 선택하면서 학습할 수 있는데, 이를 정책 기반 강화학습이라고 합니다.
정책 기반 강화학습
정책으로 행동을 선택하기 때문에 큐함수를 근사했던 딥살사의 인공신경망과는 다르게 정책 기반 강화학습에서는 인공신경망이 정책을 근사합니다.
정책을 근사하는 인공신경망을 정책신경망이라고 부릅니다. 아래 그림과 같이 정책신경망의 입력은 상태가 되고 출력은 각 행동을 할 확률이 됩니다.

출력이 각 행동을 할 확률이므로 출력층의 활성함수도 딥살사처럼 선형함수이면 안됩니다. 아래의 코드와 같이 정책신경망에서는 출력층의 활성함수로 Softmax 함수를 사용합니다.
class REINFORCE(tf.keras.Model):
def __init__(self, action_size):
super(REINFORCE, self).__init__()
self.fc1 = Dense(24, activation='relu')
self.fc2 = Dense(24, activation='relu')
self.fc_out = Dense(action_size, activation='softmax') # 딥살사와 다르게 Softmax 함수 사용
def call(self, x):
x = self.fc1(x)
x = self.fc2(x)
policy = self.fc_out(x)
return policy # 출력이 정책
Softmax 함수는 0과 1 사이의 값을 출력하고 출력층에서 나오는 출력이 다 합해서 1이 나오게 하는 함수입니다. 그렇기 때문에 정책을 출력하는 정책신경망 출력층의 활성함수로 딱 알맞은 것이죠.
폴리시 그레이디언트
인공신경망이 학습하는 것은 가중치와 편향 값이라고 했습니다. 정책신경망은 정책을 근사하기 때문에 가중치값을 바꾸면 정책이 달라지게 되겠죠.
그러면 자연스럽게 에이전트가 얻을 보상의 합도 달라지게 됩니다. 즉 누적보상은 정책신경망의 가중치에 따라 결정되는 것입니다.
강화학습의 목표는 누적보상을 최대로 하는 최적 정책을 찾는 것이었습니다. 따라서 정책신경망에 있어서 누적보상은 최적화하고자 하는 목표함수가 되고 이 목표함수의 값을 결정하는 변수는 정책신경망의 가중치가 되겠죠.
이를 수식으로 표현하면 다음과 같습니다. 목표함수는앞으로 $J(θ)$로 표현하겠습니다.
$$maximizeJ(θ)$$
딥살사에서는 오류함수를 최소화하기 위해서 경사하강법을 썼던 반면에 정책 기반 강화학습에서는 목표함수를 최대화해야 하므로 경사상승법을 사용해서 업데이트해야 합니다.
경사하강법이 오류에 대한 편미분값을 이용했다면 경사상승법은 $θ$에 대해 미분하는 그레이디언트($∇_θ$)를 이용해서 정책신경망을 업데이트할 수 있겠죠.
$$θ_{t+1} = θ_t + α∇_θJ(θ)$$
위의 수식과 같이 $θ_{t+1}$은 $θ_t$에 목표함수의 미분인 ∇_θJ(θ)의 일부분을 더한 값으로 업데이트합니다. 여기서 α는 한 번 업데이트할 때 얼마만큼 업데이트할 것인가를 정하는 학습속도입니다.
이처럼 목표함수의 경사상승법을 따라서 근사된 정책을 업데이트하는 방식을 폴리시 그레이디언트라고 합니다.
이제 저희는 목표함수를 정의하고 미분해서 정책신경망의 업데이트 식을 완성시켜야 합니다.
목표함수는 누적 보상이라고 했으니 에이전트가 특정 상태 $s_0$에 있을 때 목표함수는 상태 $s_0$에 대한 가치함수라고 할 수 있습니다.
이제 이 목표함수의 미분값을 구해야하는데 이때 사용되는 것이 폴리시 그레이디언트 정리입니다. 이 정리를 이용하면 수식은 다음과 같이 바뀝니다.
$$∇_θJ(θ) = ∇_θv_{π_θ}(s_0)$$
↓↓ 폴리시 그레이디언트 정리 사용
$$∇_θJ(θ) = \sum_sd_{π_θ}(s)\sum_a∇_θπ_θ(a | s) q_π(s, a)$$
$d_{π_θ}$는 s라는 상태에 에이전트가 있을 확률입니다. 위 수식의 의미는 가능한 모든 상태에 대해 각 상태에서 특정 행동을 했을 때 받을 큐함수의 기댓값의 미분을 의미합니다.
우변에 $π_θ(a | s)$를 곱해주고 나눠주면 식은 다음과 같습니다.
$$∇_θJ(θ) = \sum_sd_{π_θ}(s)\sum_aπ_θ(a | s) × \frac{∇_θπ_θ(a | s)}{π_θ(a | s)}q_π(s, a)$$
$\frac{∇_θπ_θ(a | s)}{π_θ(a | s)}$은 로그의 미분 형태이므로 $∇_θlogπ_θ(a | s)$로 바꿀 수 있습니다.
$$∇_θJ(θ) = \sum_sd_{π_θ}(s)\sum_aπ_θ(a | s) × ∇_θlogπ_θ(a | s) q_π(s, a)$$
위 수식에서 $\sum_sd_{π_θ}(s)\sum_aπ_θ(a | s)$는 에이전트가 "어떤 상태 s에서 행동 a를 선택할 확률"을 의미합니다. 따라서 이 수식을 기댓값의 형태로 표현할 수 있습니다.
최종적으로 목표함수의 미분은 다음과 같이 표현할 수 있습니다.
$$∇_θJ(θ) = E_{π_θ}[∇_θlogπ_θ(a | s)q_π(s, a)]$$
기댓값은 샘플링으로 대체할 수 있으므로 결국 정책신경망을 업데이트하기 위해서 $∇_θlogπ_θ(a | s) q_π(s, a)$의 값만 계산하면 되는 것이죠.
이를 정책신경망의 업데이트 식에 대입하면 다음과 같습니다.
$$θ_{t+1} = θ_t + α∇_θJ(θ) ∽ θ_t + α[∇_θlogπ_θ(a | s)q_π(s, a)]$$
하지만 위 식에서 이상한 점을 찾을 수 있습니다. 정책 기반 강화학습은 정책을 근사하여 사용하기 때문에 큐함수나 가치함수 값을 알 수 없습니다.
즉 업데이트 식에서 $q_π(s, a)$를 구할 수 없는 것이죠. 이를 해결하기 위해서 저희는 큐함수를 반환값 $G_t$로 대체하는 고전적인 방법을 사용합니다.
이렇게 큐함수를 반환값 $G_t$로 대체하여 사용하는 것을 REINFORCE 알고리즘이라고 합니다.
$$θ_{t+1} ∽ θ_t + α[∇_θlogπ_θ(a | s) G_t]$$
위의 식이 REINFORCE 알고리즘의 업데이트 식인 것입니다. 각 상태의 반환값을 구하기 위해서는 에피소드가 끝낼 때까지 기다려야 합니다.
에피소드가 끝나고 학습을 한다는 것이 몬테카를로 예측과 유사하기 때문에 이를 몬테카를로 폴리시 그레이디언트라고도 부릅니다.
REINFORCE 코드 설명
REINFORCE 알고리즘은 반환값을 이용해서 정책을 업데이트하므로 에피소드가 끝날 때까지 기다려야 합니다.
따라서 에이전트는 (현재 상태에서 행동을 선택 → 한 타임스텝 진행 → 환경으로부터 다음 상태와 보상을 받음 → 에피소드가 끝날 때까지 위의 과정을 반복 → 에피소드가 끝나면 환경으로부터 받은 정보를 이용하여 학습을 진행) 이 과정들을 거칩니다.
<행동 선택>
# 정책신경망으로 행동 선택
def get_action(self, state):
policy = self.model(state)[0]
policy = np.array(policy)
return np.random.choice(self.action_size, 1, p=policy)[0] # 정책에 따라 행동 선택정책을 근사한 정책신경망을 사용하기 때문에 행동을 선택할 때 정책신경망의 출력값을 이용하면 됩니다.
정책은 각 행동을 할 확률을 나타낸 것이기 때문에 위의 코드처럼 self.model(state)[0]로 나오는 정책 policy을 이용해서 확률에 따라 행동을 선택하는 것을 확인할 수 있습니다.
이미 확률적으로 행동을 선택하기 때문에 딥살사 알고리즘의 ε-탐욕정책과 같이 따로 탐험을 위한 작업을 해주지 않아도 됩니다.
<학습 정보 저장>
# 한 에피소드 동안의 상태, 행동, 보상을 저장
def append_sample(self, state, action, reward):
self.states.append(state[0])
self.rewards.append(reward)
act = np.zeros(self.action_size)
act[action] = 1
self.actions.append(act)에피소드가 끝나면 에피소드를 진행하면서 얻은 환경의 정보를 이용하여 학습하므로 에이전트가 지나온 상태, 선택한 행동, 환경으로부터 얻은 보상들을 저장해놓아야 합니다.
에이전트가 선택한 행동은 리스트 형태로 저장하는데, 선택한 행동에 해당하는 인덱스의 값에 1을 대입하여 저장합니다.
<반환값 계산>
# 반환값 계산
def discount_rewards(self, rewards):
discounted_rewards = np.zeros_like(rewards)
running_add = 0
for t in reversed(range(0, len(rewards))):
running_add = running_add * self.discount_factor + rewards[t]
discounted_rewards[t] = running_add
return discounted_rewardsREINFORCE 알고리즘은 반환값을 사용하기 때문에 에이전트가 지나온 상태의 반환값들을 알아야 합니다.
만약 에이전트가 하나의 에피소드에서 5개의 상태를 지나왔다면 반환값도 5개 존재할 것이고 이들의 식은 다음과 같을 것입니다.

그런데 위의 식처럼 $G_1$부터 차례대로 각 상태의 반환값을 구한다고 하면 이전 반환값 계산에 사용했던 값들이 다시 사용되는 것을 확인할 수 있습니다.
만약 반환값을 $G_5$부터 구한다면 이전 계산값을 사용할 수 있기 때문에 아래 그림과 같이 계산은 훨씬 효율적일 것입니다.

그렇기 때문에 위의 코드에서는 반복문을 이용해서, 환경으로부터 받은 마지막 보상으로 마지막 상태의 반환값부터 차례대로 구하도록 하였습니다.
<정책신경망 업데이트>
# 정책신경망 업데이트
def train_model(self):
# 반환값 정규화 과정
discounted_rewards = np.float32(self.discount_rewards(self.rewards))
discounted_rewards -= np.mean(discounted_rewards)
discounted_rewards /= np.std(discounted_rewards)
# 크로스 엔트로피 오류함수 계산
model_params = self.model.trainable_variables
with tf.GradientTape() as tape:
tape.watch(model_params)
policies = self.model(np.array(self.states))
actions = np.array(self.actions)
action_prob = tf.reduce_sum(actions * policies, axis=1)
cross_entropy = - tf.math.log(action_prob + 1e-5)
loss = tf.reduce_sum(cross_entropy * discounted_rewards)
entropy = - policies * tf.math.log(policies)
# 오류함수를 줄이는 방향으로 모델 업데이트
grads = tape.gradient(loss, model_params)
self.optimizer.apply_gradients(zip(grads, model_params))
self.states, self.actions, self.rewards = [], [], []
return np.mean(entropy)정책신경망의 업데이트 성능을 높이기 위해서 미리 구한 반환값들을 정규화해준 후 사용합니다. 이제 이 반환값들을 이용해서 오류함수를 계산하고 오류함수를 편미분 하여 정책신경망을 업데이트해줘야 합니다.
$$θ_{t+1} ∽ θ_t + α∇_θ[logπ_θ(a | s) G_t]$$
정책신경망을 업데이트하는 식을 위와 같이 표현할 수 있기 때문에 $logπ_θ(a | s) G_t$이 정책신경망의 목표가 되는 오류함수임을 알 수 있습니다.
이 오류함수의 의미를 알려면 크로스 엔트로피라는 오류함수를 알아야 합니다. 크로스 엔트로피는 엔트로피의 변형이기 때문에 엔트로피가 무엇인지부터 살펴봅시다.
엔트로피의 식은 다음과 같으며 불확실성의 정도를 나타내는 수치입니다.
엔트로피 = $-\sum_{i}\:p_i\:log\:p_i$ ($p_i$ = i번째 사건이 일어날 확률)
엔트로피 값이 클수록 데이터가 혼재되어 있어 어떤 값이 나올지 예측하기 어렵다는 뜻입니다.
크로스 엔트로피는 엔트로피의 식에서 살짝 변형되어 현재 예측 값이 얼마나 정답과 가까운지를 나타내는 수치로 식은 다음과 같습니다.
크로스 엔트로피 = $-\sum_{i}\:y_i\:log\:p_i$ ($y_i$ = 정답, $p_i$ = 예측 값)
정답과 예측 값이 가까워질수록 크로스 엔트로피 값은 최소가 되는 특징이 있기 때문에 이를 오류함수로 사용할 수 있는 것이죠.
폴리시 그레이디언트에서는 에이전트가 실제로 선택한 행동을 정답으로 두어 크로스 엔트로피의 식은 다음과 같습니다.
크로스 엔트로피 = $-\sum_{i}\:y_i\:log\:p_i$ → $-\:log\:p_{action}$
에이전트가 실제로 선택한 행동의 값만 $y_i$가 1이고 나머지는 0이 되므로 위의 식처럼 되는 것이죠.
policies = self.model(np.array(self.states))
actions = np.array(self.actions)
action_prob = tf.reduce_sum(actions * policies, axis=1)
cross_entropy = - tf.math.log(action_prob + 1e-5)
따라서 코드도 위와 같이 작성되었습니다. actions는 실제로 한 행동만 1이 되는 원-핫 벡터이기에 현재 상태에서의 정책 policies와 곱하면 실제로 한 행동에 해당하는 확률값을 구할 수 있습니다.
이 확률값에 log를 취한 것이 cross_entropy가 되는 것이죠. 이 크로스 엔트로피 값만을 이용해서 정책신경망을 업데이트한다면 무조건 에이전트가 실제로 한 행동을 더 선택하는 방향으로 업데이트될 것입니다.
하지만 만약 에이전트가 실제로 한 행동이 안 좋은 행동이라면 그 행동을 할 확률을 낮춰야 합니다. 이를 위해서 행동의 좋고 나쁨의 정보를 가지고 있는 반환값을 곱해주는 것이죠.
반환값이 양수라면 에이전트의 행동이 이득을 줬다는 뜻이므로 에이전트가 선택한 행동을 할 확률을 높이고, 음수라면 안 좋은 행동이었다는 뜻이므로 에이전트가 선택한 행동을 할 확률을 낮출 것입니다.
크로스 엔트로피에 반환값을 곱한 loss가 최종 오류함수가 됩니다.
이제 이 오류함수에 대해 그레이디언트를 구해 정책신경망을 업데이트하면 됩니다.
from tensorflow.keras.optimizers import Adam
#생략
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# 오류함수를 줄이는 방향으로 모델 업데이트
grads = tape.gradient(loss, model_params)
self.optimizer.apply_gradients(zip(grads, model_params))업데이트 코드는 위와 같습니다. 하지만 여기서 이상한 점이 하나 있습니다.
분명 정책 기반 강화학습은 목표함수를 최대화해야 하므로 경사상승법을 사용한다고 했는데 위 코드는 경사하강법 중 하나인 Adam을 사용하고 있습니다.
이는 저희가 오류함수로 $logπ_θ(a | s) G_t$가 아닌 $-logπ_θ(a | s) G_t$를 사용했기 때문입니다.
$$θ_{t+1} ∽ θ_t + α[∇_θlogπ_θ(a | s) G_t] = θ_t - α[∇_θ(-logπ_θ(a | s) G_t)]$$
즉 REINFORCE 알고리즘의 정책신경망 업데이트 식이 위와 같이 되기 때문에 경사하강법인 Adam을 사용하여 가중치 값을 업데이트하는 것입니다.
REINFORCE의 전체 코드는 아래 링크에서 확인할 수 있습니다.
https://github.com/rlcode/reinforcement-learning-kr-v2
GitHub - rlcode/reinforcement-learning-kr-v2: [파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판
[파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판 예제. Contribute to rlcode/reinforcement-learning-kr-v2 development by creating an account on GitHub.
github.com
REINFORCE의 실행 및 결과

코드를 실행시키면 터미널 창에는 에피소드, 점수, 엔트로피 값이 출력됩니다. 엔트로피는 현재 모델이 얼마나 모험을 하고 있는지 간접적으로 알려주는 값입니다.
에이전트는 초반에 장애물에 많이 부딪히게 되어 장애물에 부딪히지 않도록 학습합니다. 에이전트는 장애물에 부딪히지 않기 위해서 시작점에서 움직이지 않게 될 수도 있습니다.
이를 방지하기 위해서 이 코드에서는 타임스텝마다 (-0.1)의 보상을 에이전트에게 주어 시작점에 머무는 행동이 좋은 행동이 아님을 학습하게 했습니다.
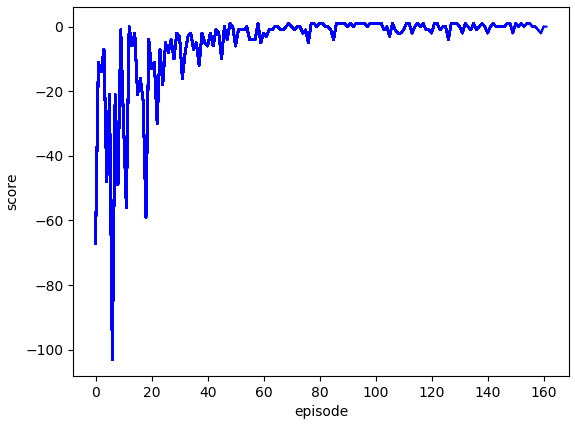
위의 그림은 약 150 에피소드를 진행시켰을 때 에이전트가 얻은 점수 그래프입니다. 타임스텝마다 (-0.1)의 보상을 주기 때문에 딥살사와는 다르게 수렴하는 점수가 1이 아닌 것을 확인할 수 있습니다.
다음 포스팅에서는 브레이크아웃 게임에 사용되었던 DQN 인공신경망을 새로운 카트폴이라는 예제에 적용시켜보면서 설명하도록 하겠습니다. 읽어주셔서 감사합니다~!

http://www.yes24.com/Product/Goods/44136413
파이썬과 케라스로 배우는 강화학습 - YES24
“강화학습을 쉽게 이해하고 코드로 구현하기”강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다!‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지기
www.yes24.com
※ 이 글은 위의 책 내용을 바탕으로 작성한 글입니다.
'강화학습 > 파이썬과 케라스로 배우는 강화학습(스터디)' 카테고리의 다른 글
| [강화학습] 13 - 액터-크리틱 (0) | 2023.01.18 |
|---|---|
| [강화학습] 12 - DQN 알고리즘(Cartpole) (0) | 2023.01.11 |
| [강화학습] 10 - 딥살사(DeepSARSA) (1) | 2023.01.03 |
| [강화학습] 09 - 인공신경망 (0) | 2022.12.30 |
| [강화학습] 08 - 큐러닝(QLearning) (2) | 2022.12.28 |