개요
이전 포스팅에서는 첫 번째 강화학습 알고리즘인 살사에 대해서 배웠습니다. 살사는 ε-탐욕 정책으로 행동하면서 샘플 $[S_t,A_t,R_{t+1},S_{t+1},A_{t+1}]$을 모으고 이 샘플을 이용해서 시간차 제어 식으로 큐함수를 업데이트하는 과정을 반복하였습니다. $$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + α(R_{t+1} + γQ(S_{t+1},A_{t+1})) - Q(S_t,A_t))$$
하지만 이런 살사를 이용해서 에이전트를 학습시키다보면 잘못된 정책을 학습하는 경우가 생깁니다.
이번 포스팅에서는 살사의 한계와 이를 극복하기 위해 만들어진 2번째 강화학습 알고리즘, 큐러닝을 예시 코드와 함께 살펴보겠습니다.
살사의 한계
살사는 충분한 탐험을 하기 위해서 ε-탐욕 정책을 사용했습니다. 앞에서는 이 ε을 0.1로 지정해서 10% 확률로 에이전트가 탐험할 수 있도록 만들었죠.
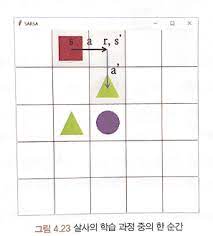
만약 에이전트가 위의 그림처럼, 현재 상태(s)에서는 탐욕 정책으로 오른쪽으로 가는 행동(a)을 선택하고 다음 상태(s')에서는 탐험을 하여 장애물인 초록색 삼각형으로 가는 아래쪽 행동(a')을 선택했다고 가정해봅시다.
에이전트의 현재 상태(s)에 대한 행동(a)의 큐함수는 다음 식으로 업데이트 될 것입니다.
$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + α(R_{t+1} + γQ(S_{t+1},A_{t+1})) - Q(S_t,A_t))$$
이때 $Q(S_{t+1},A_{t+1})$은 에이전트가 다음 상태(s')에서 장애물로 가는 아래쪽 행동(a')의 큐함수를 뜻하므로 값이 낮을 것입니다.
따라서 현재 상태(s)에 대한 행동(a)의 큐함수 즉 현재 상태에서 오른쪽으로 가는 행동의 큐함수의 값도 함께 낮아지게 되는 것이죠.
이로 인해서 다음 에피소드에서 에이전트가 이전과 똑같은 상태(s)에 위치해 있다면, 다시 탐험을 하지 않는 이상 낮아진 큐함수로 인해서 오른쪽으로 가는 행동은 선택하지 않을 것입니다.
그러면 아래 그림과 같이 에이전트는 오른쪽으로 가지 않고 일종의 갇혀버리는 현상이 발생할 수 있습니다.

결국 이런 살사의 문제점은 ε-탐욕 정책 때문에 최적 정책을 학습하지 못하고 잘못된 정책을 학습했습니다.
하지만 그렇다고 강화학습에 있어서 탐험을 없앨 순 없습니다. 탐험의 문제로 최적 정책을 학습하지 못할거니까 말이죠.
이러한 딜레마를 해결하기 위해 사용하는 것이 오프폴리시 시간차 제어, 다른 말로는 큐러닝입니다.
큐러닝
오프폴리시의 뜻은 현재 행동과는 독립적으로 학습한다는 것입니다. 즉 에이전트의 행동과는 별개로 따로 목표 정책을 둬서 학습은 목표 정책에 따라서 합니다.
반대로 자신이 행동하는 대로 학습하는 것을 온폴리시라고 하는데, 이전에 배운 살사가 바로 이 온폴리시 시간차 제어입니다.
에이전트가 현재 상태 s에서 ε-탐욕 정책으로 행동 a를 선택하고 환경으로부터 보상 r과 다음 상태 s'을 받는 것까지는 살사와 큐러닝이 동일합니다.
하지만 살사는 다음 상태 s'에서 다시 ε-탐욕 정책으로 다음 행동 a'을 선택하고 이를 이용해서 큐함수를 업데이트했다면, 큐러닝은 다음 상태 s'에서 실제로 어떤 행동을 선택할지에 상관없이 가장 큰 큐함수를 현재 큐함수의 업데이트에 사용합니다.
즉 살사에서 필요한 샘플이 $[s, a, r, s', a']$이었다면, 큐러닝에서는 a'을 제외한 $[s, a, r, s']$만 필요한 것이죠. ($Q(S_{t+1},A_{t+1})$의 값이 다음 상태(s')에서의 큐함수 최댓값으로 정해져 있기 때문에 a'은 필요가 없습니다.)
이 큐러닝의 큐함수 업데이트 식은 다음과 같습니다.
$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + α(R_{t+1} + γ\underset{a'}{max}Q(S_{t+1},a')) - Q(S_t,A_t))$$
식을 자세히 보면 $R_{t+1} + γ\underset{a'}{max}Q(S_{t+1},a')$ 부분이 벨만 최적 방정식과 비슷하다는 것을 느꼈을 것입니다.
살사가 큐함수를 업데이트하기 위해서 벨만 기대 방정식을 사용했다면 큐러닝에서는 큐함수 업데이트를 위해서 벨만 최적 방정식을 사용한 것이죠.

큐러닝을 통해서 에이전트가 학습한다면, 살사 때처럼 다음 상태(s')에서 ε-탐욕 정책을 통해 한 행동이 장애물로 가는 안 좋은 행동이더라도 이는 학습에 영향을 끼치지 않으므로 잘못된 정책으로 학습하지 않을 것입니다.
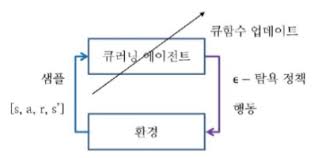
즉 큐러닝은 살사와 유사하지만 ε-탐욕 정책에 의한 살사의 한계를 벨만 최적 방정식을 이용하여 해결한 것이죠. 큐러닝의 학습 과정은 다음과 같습니다.
큐러닝 코드 설명
큐러닝과 살사의 차이점은 큐함수를 업데이트하는 식과 사용하는 샘플밖에 없습니다. 따라서 큐러닝을 업데이트하는 코드만을 설명하도록 하겠습니다. 이외의 코드는 이전 살사의 코드 설명을 참고해주시길 바랍니다.
https://developer-lionhong.tistory.com/15
[강화학습] 07 - 살사(SARSA)
개요 처음부터 지금까지 꽤 많은 것을 배웠지만 충격적이게도 이 살사부터를 실제 강화학습 알고리즘입니다. ( ← 제가 처음 이 내용 접했을 당시 표정이었습니다 엌ㅋㅋㅋㅋㅋ) 이전에 배웠던
developer-lionhong.tistory.com
<큐함수 업데이트>
# <s, a, r, s'> 샘플로부터 큐함수 업데이트
def learn(self, state, action, reward, next_state):
state, next_state = str(state), str(next_state)
q_1 = self.q_table[state][action]
# 벨만 최적 방정식을 사용한 큐함수의 업데이트
q_2 = reward + self.discount_factor * max(self.q_table[next_state])
self.q_table[state][action] += self.step_size * (q_2 - q_1)큐함수를 업데이트하기 위한 샘플로 a'을 제외한 $[s, a, r, s']$만을 이용하는 것을 볼 수 있습니다.
$$Q(S_t,A_t) \leftarrow Q(S_t,A_t) + α(R_{t+1} + γ\underset{a'}{max}Q(S_{t+1},a')) - Q(S_t,A_t))$$
이후 위의 식에 따라서 max(self.q_table[next_state]), 다음 상태의 큐함수 최댓값으로 큐함수를 업데이트하는 것도 확인할 수 있습니다.
큐러닝의 전체 코드는 아래 링크에서 찾아볼 수 있습니다.
https://github.com/rlcode/reinforcement-learning-kr-v2
GitHub - rlcode/reinforcement-learning-kr-v2: [파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판
[파이썬과 케라스로 배우는 강화학습] 텐서플로우 2.0 개정판 예제. Contribute to rlcode/reinforcement-learning-kr-v2 development by creating an account on GitHub.
github.com
큐러닝 코드의 실행 결과
큐러닝 코드를 실행시킨 결과와 살사의 결과를 비교해보면 다음과 같습니다. 왼쪽이 살사의 실행 결과이고 오른쪽이 큐러닝의 실행 결과입니다.
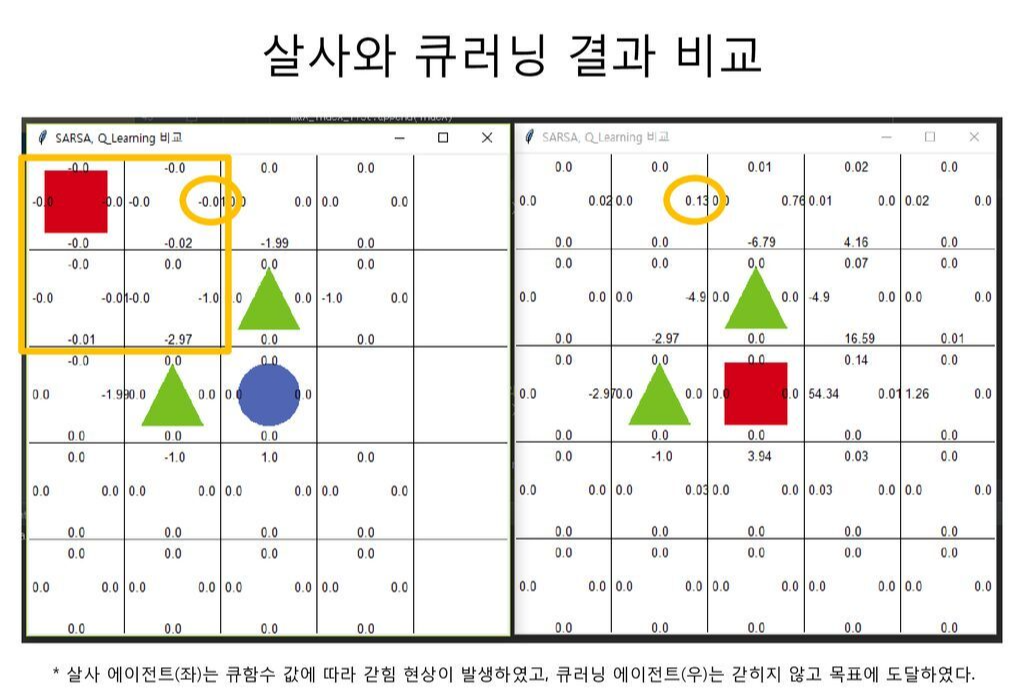
살사의 실행 결과에서 동그라미 친 부분을 살펴보면 큐함수가 음수인 것을 확인할 수 있습니다.
이는 에이전트가 다음 상태(s')에서 ε-탐욕 정책을 통해 했던, 장애물로 가는 좋지 않은 행동이 현재 상태의 큐함수 업데이트에 영향을 미쳤기 때문입니다.
이로 인해서 에이전트는 탐험을 하지 않는 한 사각형 안에 있는 상태에 갇히고 맙니다.
하지만 큐러닝의 실행 결과를 보면 큐함수가 양수인 것을 확인할 수 있습니다. 이는 아무리 에이전트가 다음 상태(s')에서 좋지 않은 행동을 하더라고 현재 상태의 큐함수 업데이트에 영향을 끼치지 않기 때문입니다.
따라서 에이전트는 같히지 않고 벗어나는 정책을 학습합니다.
저희는 지금까지 환경의 모델없이 학습하는 2가지 강화학습에 대해서 배웠습니다. 하지만 이 두 방법으로는 상태가 많고 환경이 계속해서 변하는 복잡한 문제에는 적용할 수 없습니다.
바로 살사와 큐러닝으로는 계산 복잡도와 차원의 저주를 해결하지 못하기 때문인데요.
이를 해결하기 위해서 나온 것이 바로 인공신경망입니다. 다음 시간에는 살사와 큐러닝의 한계와 함께 인공신경망에 대해서 설명하도록 하겠습니다. 오늘도 읽어주셔서 감사합니다!!

http://www.yes24.com/Product/Goods/44136413
파이썬과 케라스로 배우는 강화학습 - YES24
“강화학습을 쉽게 이해하고 코드로 구현하기”강화학습의 기초부터 최근 알고리즘까지 친절하게 설명한다!‘알파고’로부터 받은 신선한 충격으로 많은 사람들이 강화학습에 관심을 가지기
www.yes24.com
※ 이 글은 위의 책 내용을 바탕으로 작성한 글입니다.
'강화학습 > 파이썬과 케라스로 배우는 강화학습(스터디)' 카테고리의 다른 글
| [강화학습] 10 - 딥살사(DeepSARSA) (1) | 2023.01.03 |
|---|---|
| [강화학습] 09 - 인공신경망 (0) | 2022.12.30 |
| [강화학습] 07 - 살사(SARSA) (4) | 2022.12.27 |
| [강화학습] 06 - 몬테카를로와 시간차 예측 (2) | 2022.12.24 |
| [강화학습] 05 - 그리드월드와 다이내믹 프로그래밍 (2) (5) | 2022.12.22 |